Konubinix' site

Recherche Reproductible D'un Prénom

Table des matières

Introduction

Je suis depuis quelque mois un cours en ligne ouvert massif sur la recherche reproductible. Il est demandé de produire un document d’analyse mettant en pratique les acquis sur le sujet.

Or, je vais être papa de mon troisième enfant en février (un garçon). Trouver un prénom est toujours un sujet délicat. On veut que le prénom soit original, mais aussi qu’il soit facile à porter (donc pas si original que ça).

Je suis parti de l’observation que ma compagne, Aurélie, n’aime pas son prénom, qu’elle trouve trop commun. Or, j’aime mon prénom (Samuel) et pense que c’est en parti due au fait qu’il correspond au critère indiqué précédemment.

Je formule donc l’hypothèse suivante : Le prénom que nous aurons envie de choisir pour notre fils devrait être moins commun que Aurélie à l’époque de sa naissance, et peut être au moins aussi commun que Samuel à l’époque de sa naissance.

Bien sûr, cette hypothèse est ni formelle (combien font suffisamment et trop ?), ni vérifiable (si mon enfant aime son prénom, comment vérifier que c’est dû à ce critère ?). Peu importe, c’est surtout l’occasion de :

  1. faire un exercice de manipulation de données (avec pandas),
  2. faire un exercice de recherche reproductible,
  3. et me permettre de me brasser des prénoms pour m’aider dans mon choix.

Configuration

L’analyse est faite intégralement en python3, avec la bibliothèque pandas donc je dois informer emacs de ce fait.

(setq org-babel-python-command "python3")

"python3"

Pour assurer de reproduire ces résultats, voici la version de pandas utilisée.

import pandas
pandas.__version__

1.1.5

Afin de reproduire un environnement propice à reconstruire cette étude, voici un exemple de fichier nix a utiliser.

with import <nixpkgs> {};

pkgs.mkShell {
  inputsFrom = with pkgs; [ emacs python37.pkgs.pandas ];
}

Récupération de données

Pour identifier l’aspect « commun » du prénom, nous allons utiliser une base de données de nombre de naissances par année en France.

Cette base est disponible sous la forme d’un fichier au format json dont le chemin ipfs est : /ipfs/bafybeigtew7dm2y7ijmc44nam4kf6rfcnisdps35bpo4i435o6zmxcjofi

Vous pouvez remarquer que, comme il s’agit d’un lien ipfs, cette analyse est garanti de toujours utiliser la même donnée. Ce fichier est disponible en permanence sur le réseau (tant que des nœuds du réseau hébergeront ce fichier). Ceci colle bien, selon moi, avec l’idée de recherche reproductible. Ce lien est disponible (au moins) sur un nœud publique ipfs (le miens). Vous pouvez le récupérer en démarrant votre noeud ipfs ou en allant le chercher sur un gateway publique.

Première impression

Commençons par charger le fichier en mémoire pour voir à quoi il ressemble.

import pandas
data = pandas.read_json(url)
print(data.describe())
print(data.head())

       forename   sex                                             births forenameUnique    id alternatives
count      1487  1487                                               1487           1487  1487          558
unique     1474     2                                               1487           1487  1486          556
top        Eden     f  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 5, ...          Nawel   mae       [Éden]
freq          2   829                                                  1              1     2            2
     forename sex                                             births forenameUnique          id alternatives
0       Aaron   m  [0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...          Aaron       aaron          NaN
1    Abdallah   m  [0, 0, 4, 6, 10, 7, 8, 12, 17, 20, 24, 21, 25,...       Abdallah    abdallah          NaN
2       Abdel   m  [0, 0, 6, 7, 5, 8, 15, 17, 23, 37, 35, 43, 54,...          Abdel       abdel          NaN
3   Abdelaziz   m  [0, 0, 0, 0, 0, 3, 0, 0, 8, 4, 12, 17, 14, 12,...      Abdelaziz   abdelaziz          NaN
4  Abdelkader   m  [0, 5, 3, 8, 9, 13, 13, 15, 30, 51, 52, 69, 72...     Abdelkader  abdelkader          NaN

On peut voir que le fichier contient 1487 prénoms, dont les nombres de naissances sont donnés par année à la colonne birth. L’id permet de retrouver le prénom, donc nous n’auront pas besoin des détails cosmétiques fournis par forenameUnique, forename ou alternatives. Les donnés sont censées donner les historiques de naissances de 1950 à 2015.

Premier nettoyage

Comme nous allons nous concentrer sur l’id du prénom, assurons nous d’abord qu’il est bien unique.

data.id.is_unique

False

Hmmm, regardons quels prénoms sont en double.

count = data.groupby("id").id.count()
count[count > 1]

id
mae    2
Name: id, dtype: int64

Et regardons ce qui les différencie

data[data.id == "mae"]

    forename sex                                             births forenameUnique   id            alternatives
864      Mae   f  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...            Mae  mae  [Mahé, Maé, Maë, Mahe]
865      Maé   m  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...            Maé  mae              [Mae, Maë]

Il s’agit d’un prénom mixte. Suffixons l’id avec l’information de genre.

data.loc[data.id == "mae", "id"] = data.loc[data.id == "mae", "id"] + "-" + data.loc[data.id == "mae", "sex"]
data[data.id.str.startswith("mae-")]

    forename sex                                             births forenameUnique     id            alternatives
864      Mae   f  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...            Mae  mae-f  [Mahé, Maé, Maë, Mahe]
865      Maé   m  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...            Maé  mae-m              [Mae, Maë]

data.id.is_unique

True

Ok, tout va mieux.

Vérification les nombres de naissances

L’autre information important et le nombre de naissances. Assurons nous qu’il est bien homogène.

data.births.apply(len).unique()

[71]

Tous les prénoms ont bien 71 valeurs de naissance.

data.births.apply(lambda births: all(value >= 0 for value in births)).unique()

[ True]

Toutes le valeurs sont des entiers positifs.

Formatage des séries temporelles

Pour avoir les séries temporelles des naissances par prénom. Nous allons tout d’abord exploser la colonne births, c’est à dire la transformer en autant de ligne que d’éléments dans la liste. Puis nous allons regrouper les tables par prénom. Enfin, pour chaque group, nous allons assigner un index correspondant à l’intervalle [1950, 2015].

def to_time_series(data):
    return pandas.DataFrame(
        {
            id: d.births.values
            for id, d in data.explode("births").groupby("id")
        },
        index=pandas.date_range("1945", freq="Y", periods=71),
        dtype=int,
    )

ts_data = to_time_series(data)

ts_data

            aaron  abdallah  abdel  abdelaziz  abdelkader  abdelkrim  abdellah  abdoulaye  abel  achille  adam  adel  adelaide  ...  yvette  yvon  yvonne  zacharie  zahra  zakaria  zelie  zeynep  zina  zineb  zinedine   zoe  zohra
1945-12-31      0         0      0          0           0          0         0          0   107       29     9     0        12  ...    3368   838    1276         8      0        0      0       0     6      0         0     3      0
1946-12-31      0         0      0          0           5          0         0          0   125       36    11     0        26  ...    4689  1239    1633        12      3        0      5       0     6      0         0     6      4
1947-12-31      0         4      6          0           3          0         0          0   120       40    11     0        13  ...    4097  1269    1318         5      0        0      6       0     8      0         0     7      0
1948-12-31      0         6      7          0           8          0         0          0   108       51     7     0        15  ...    3827  1360    1297         5      0        0      0       0     8      0         0    10      7
1949-12-31      3        10      5          0           9          0         0          0   108       46    10     0        15  ...    3450  1203    1132         6      4        0      4       0    10      0         0     5      6
...           ...       ...    ...        ...         ...        ...       ...        ...   ...      ...   ...   ...       ...  ...     ...   ...     ...       ...    ...      ...    ...     ...   ...    ...       ...   ...    ...
2011-12-31   1761       187     52         20          75          7        84        116   303      396  3658   211        87  ...       0     8       0       168    156      484    700      93    62    115        80  3638     84
2012-12-31   1724       203     81         20          65          4        79        123   399      379  4155   267       116  ...       0     6       5       165    133      515    765      88    64    116        71  3457     89
2013-12-31   1908       250     65         23          56          4        70        149   432      375  4398   284       108  ...       5     6       3       197    139      506    725     122    56    124        72  3344     72
2014-12-31   2053       265     69         10          74         10        82        128   451      353  4558   252       112  ...       0     8       6       162    149      545    711     142    64    109        53  3302     99
2015-12-31   2159       303     72         18          62          6        79        136   499      374  4529   298        90  ...       0     3       5       168    138      586    708     136    71    106        51  2865     73

[71 rows x 1487 columns]

Maintenant, nous allons pouvoir jouer avec les données.

Uniquement les nom masculins

Nous voulons commencer par supprimer les prénoms mixte et féminins. Nous gardons ts_data pour apprendre, mais le résultat final n’utilisera que ces prénoms.

sample = to_time_series(data[data["sex"] == "m"])
sample

            aaron  abdallah  abdel  abdelaziz  abdelkader  abdelkrim  abdellah  abdoulaye  abel  achille  adam  adel  adem  adil  ...  yazid  yoann  yoni  youcef  younes  youri  youssef  yusuf  yvan  yves  yvon  zacharie  zakaria  zinedine
1945-12-31      0         0      0          0           0          0         0          0   107       29     9     0     0     0  ...      0      0     0       0       0      0        0      0   311  4048   838         8        0         0
1946-12-31      0         0      0          0           5          0         0          0   125       36    11     0     0     0  ...      0      0     0       0       0      0        3      0   418  6218  1239        12        0         0
1947-12-31      0         4      6          0           3          0         0          0   120       40    11     0     0     0  ...      0      0     0       0       0      0        0      0   385  6422  1269         5        0         0
1948-12-31      0         6      7          0           8          0         0          0   108       51     7     0     0     0  ...      0      0     0       4       0      0        0      0   360  6348  1360         5        0         0
1949-12-31      3        10      5          0           9          0         0          0   108       46    10     0     0     0  ...      0      0     0       4       0      0        0      0   356  6329  1203         6        0         0
...           ...       ...    ...        ...         ...        ...       ...        ...   ...      ...   ...   ...   ...   ...  ...    ...    ...   ...     ...     ...    ...      ...    ...   ...   ...   ...       ...      ...       ...
2011-12-31   1761       187     52         20          75          7        84        116   303      396  3658   211   548   164  ...     87    837    97     155     902     55      623    293   185    26     8       168      484        80
2012-12-31   1724       203     81         20          65          4        79        123   399      379  4155   267   660   141  ...     82    753   102     176    1052     47      721    256   171    19     6       165      515        71
2013-12-31   1908       250     65         23          56          4        70        149   432      375  4398   284   661   149  ...     94    617   129     189     998     56      783    314   144    33     6       197      506        72
2014-12-31   2053       265     69         10          74         10        82        128   451      353  4558   252   764   146  ...     97    542    92     221    1097     65      811    385   188    25     8       162      545        53
2015-12-31   2159       303     72         18          62          6        79        136   499      374  4529   298   761   136  ...     97    441    80     229    1022     53      992    401   149    21     3       168      586        51

[71 rows x 658 columns]

Il nous reste 657 prénoms à analyser.

Mis en place du stockage des images

J’utilise ipfs pour stocker tous mes documents, les résultat de cette étude y compris.

J’utilise donc une routine qui enverra les résultats dans ipfs.

import subprocess
from matplotlib import pyplot as plt

def save(name):
  path = f"/tmp/{name}.png"
  plt.savefig(path)
  path = subprocess.check_output(["ipfs", "add", "--quieter", "--pin=false", path], encoding="utf-8")
  return "ipfs:" + path.strip() + f"?{name}.png"

Enfin, dans le cas particulier où je voudrais regarder juste un prénom, voici une routine pour faciliter cela.

plt.figure()
ts_data[nom].plot()
plt.title(nom)
save(nom)

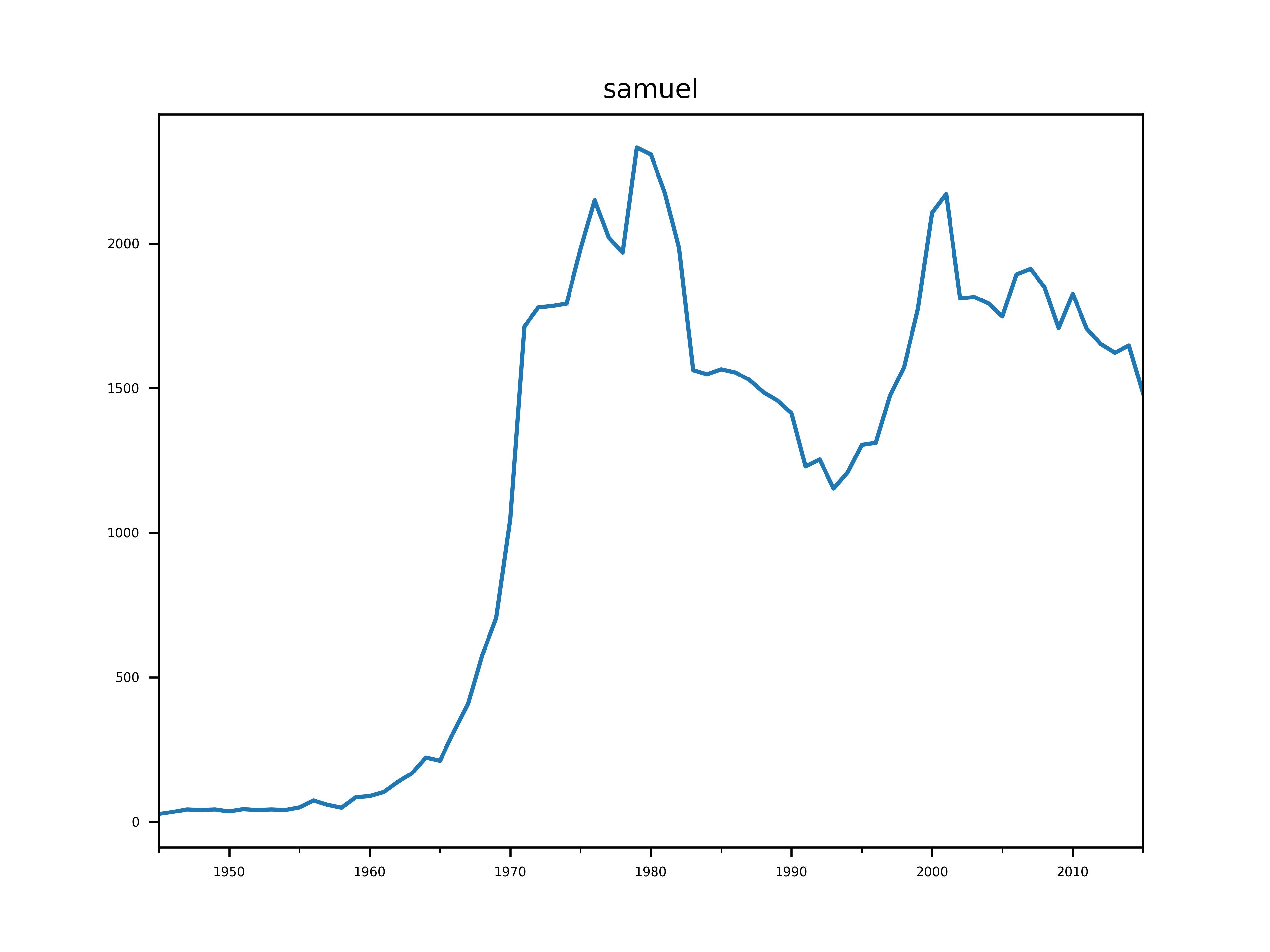
Jetons un œil aux données

Jetons d’abord de plus prêt l’allure de la dispersion des données.

plt.figure()
ts_data["moyenne"] = ts_data.mean(axis=1)
ax = ts_data[["moyenne"]].plot()
plt.fill_between(ts_data.index, ts_data["moyenne"], ts_data["moyenne"] + ts_data.std(axis=1), alpha=0.2)
plt.fill_between(ts_data.index, ts_data["moyenne"], ts_data["moyenne"] - ts_data.std(axis=1), alpha=0.2)
save("repartition")

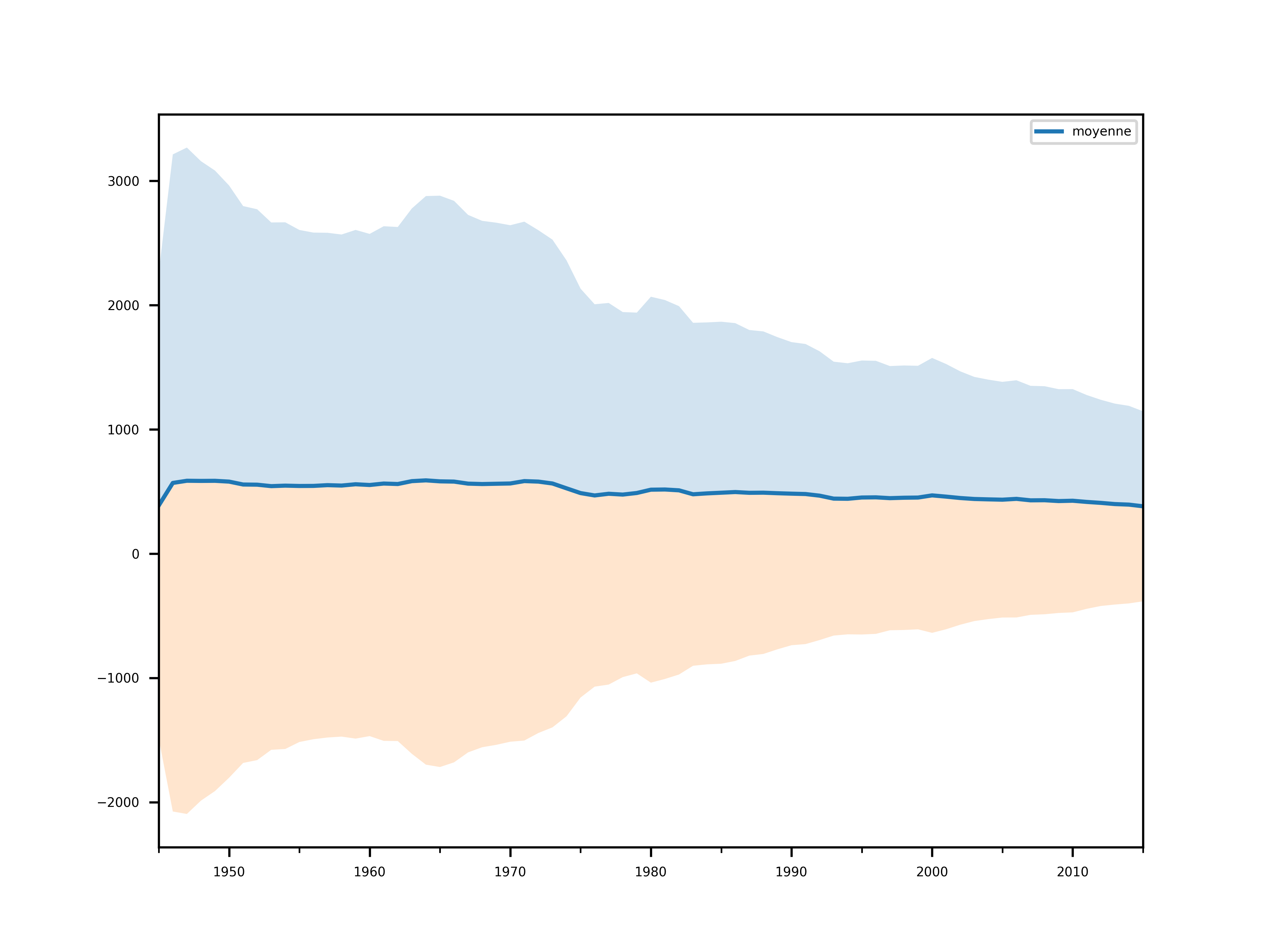
Ok, les données semblent assez homogènes. Nous allons probablement de tout la dedans.

Regardons les historiques des naissances des Samuel et Aurélie, pour avoir une idée des courbes de prénoms à rejeter et celles à garder.

from datetime import datetime
import matplotlib.pyplot as plt
ts_data[["samuel", "aurelie"]].plot(color=["blue", "orange"])
plt.annotate("Naissance Aurélie",
             (datetime(year=1985, month=5, day=9), 0),
             (-1500, 200),
             'data',
             'offset pixels',
             arrowprops={"width": 1}
)
plt.annotate("Naissance Samuel",
             (datetime(year=1987, month=6, day=24), 0),
             (-1000, 500),
             'data',
             'offset pixels',
             arrowprops={"width": 1}
)
plt.axvline(datetime(year=1987, month=6, day=24), color="blue")
plt.axvline(datetime(year=1985, month=5, day=9), color="orange")
save("refs")

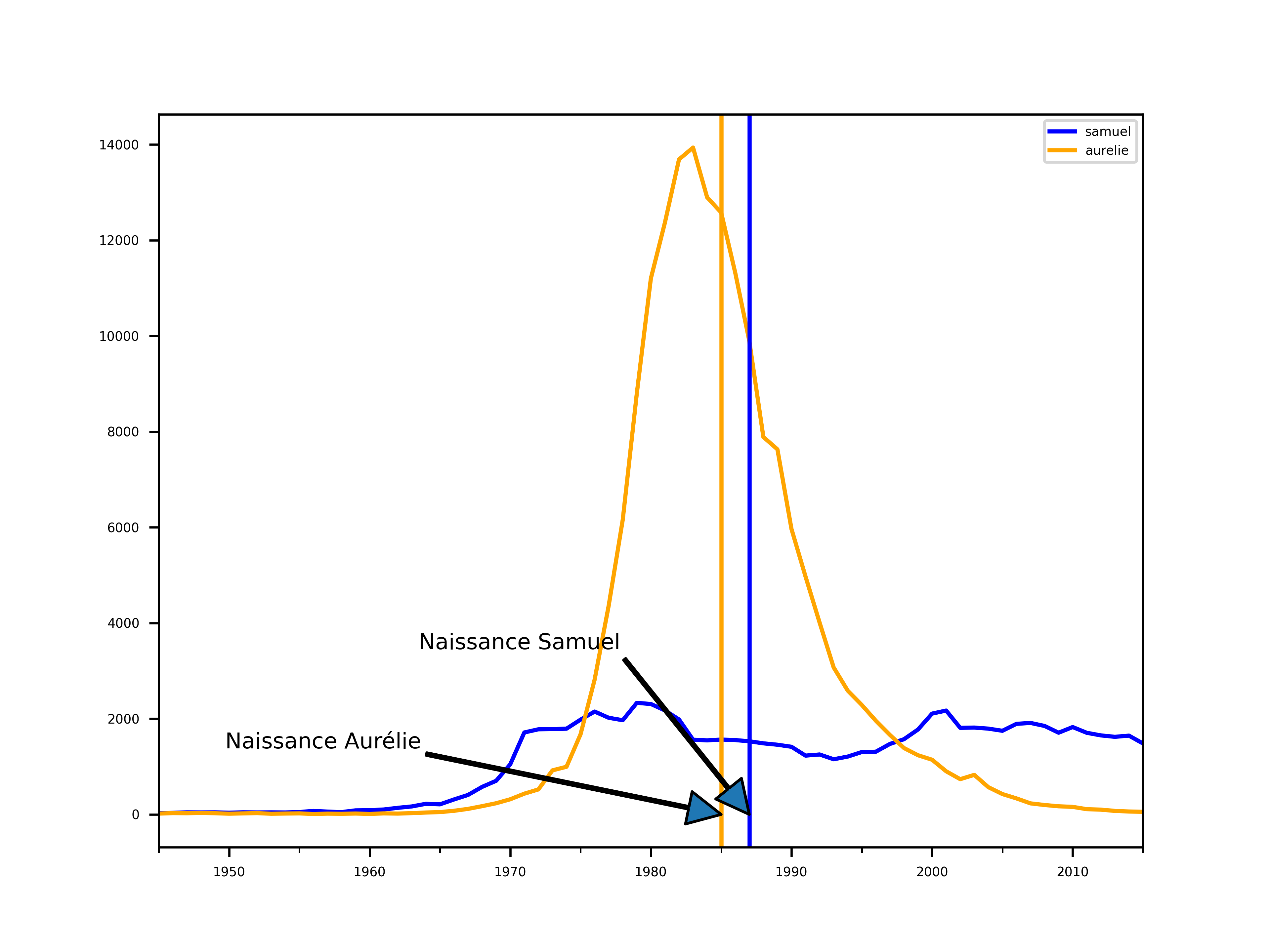
Hmm, on peu voir deux choses:

  1. les ordres de grandeurs à la naissance sont différents (~2000 pour ~12000)
  2. les deux naissances ont lieu juste après un phénomène de mode

La courbe de Samuel étant aplatie, regardons la de plus prêt.

plt.figure()
ts_data[["samuel"]].plot(color="blue")
plt.annotate("Naissance Samuel",
             (datetime(year=1987, month=6, day=24), 0),
             (-1000, 500),
             'data',
             'offset pixels',
             arrowprops={"width": 1}
)
plt.axvline(datetime(year=1987, month=6, day=24), color="blue")
save("samuel")

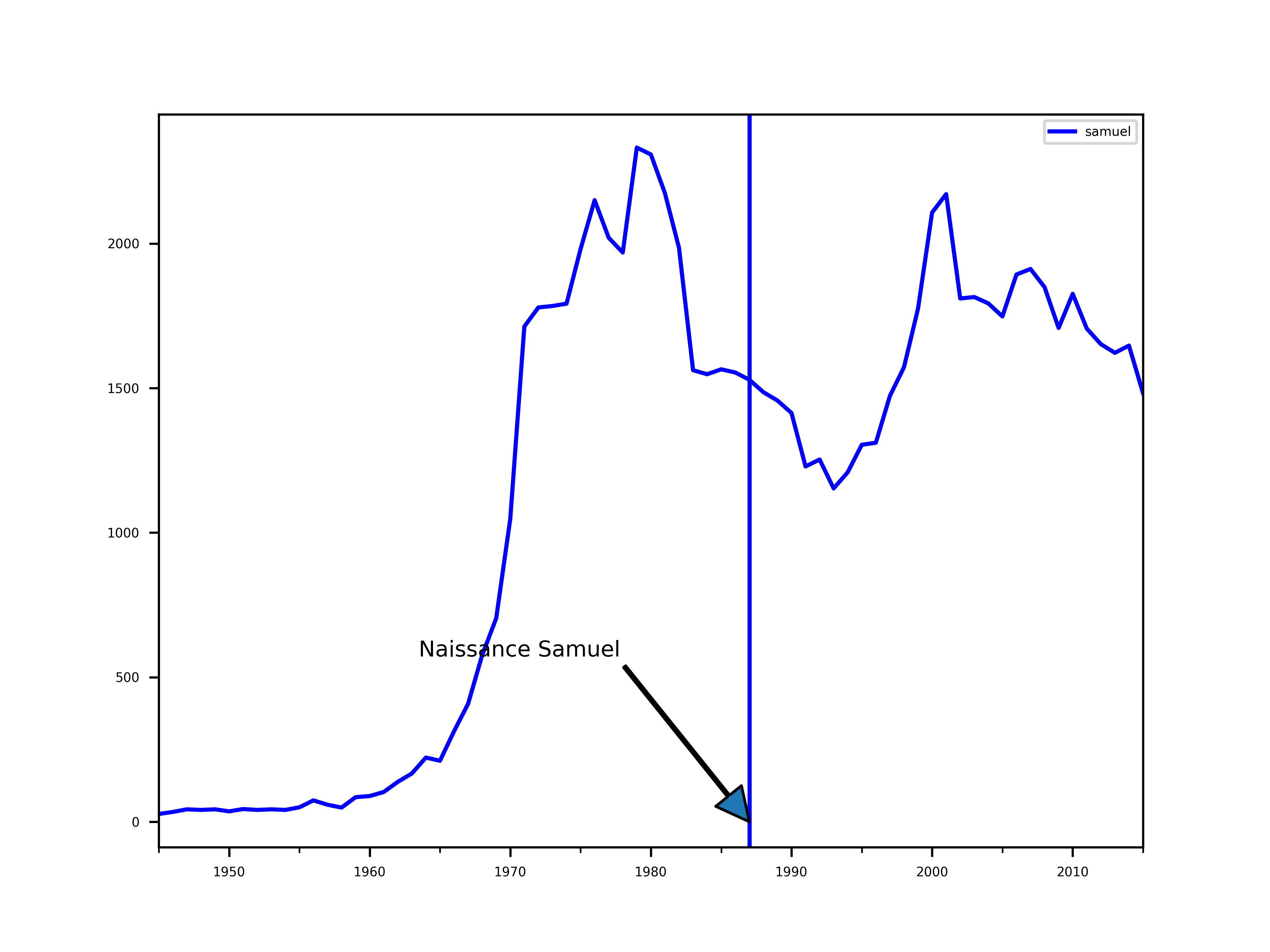
On sent effectivement le pic de Samuel dans les années 70, avant la naissance.

Première hypothèse : impact du nombre de naissances proche de la fin

Émettons l’hypothèse que, indépendant de la présence d’un phénomène de mode, c’est la quantité de naissances qui impactera le sentiment d’appropriation du prénom. Trop faible, le prénom semblera marginal, trop élevé, le prénom semblera trop commun. Sur la base des ressentis subjectifs de Samuel et Aurélie, imaginons qu’un prénom satisfaisant aura une valeur autour de 2000 à la naissance.

Le bébé est prévu début 2021, soit à peu prêt 5 ans après la dernière données.

Essayons de nous faire une idée de l’information qu’apporte les courbes en regardant à quoi ressemblaient les courbes 5 ans avec les naissances de Samuel et Aurélie.

plt.figure()
samuel_no_data = ts_data.loc[:datetime(year=1981, month=1, day=1), "samuel"]
aurelie_no_data = ts_data.loc[:datetime(year=1979, month=1, day=1), "aurelie"]
pandas.concat([samuel_no_data, aurelie_no_data], axis=1).plot()
save("samuel_aurelie_no_data")

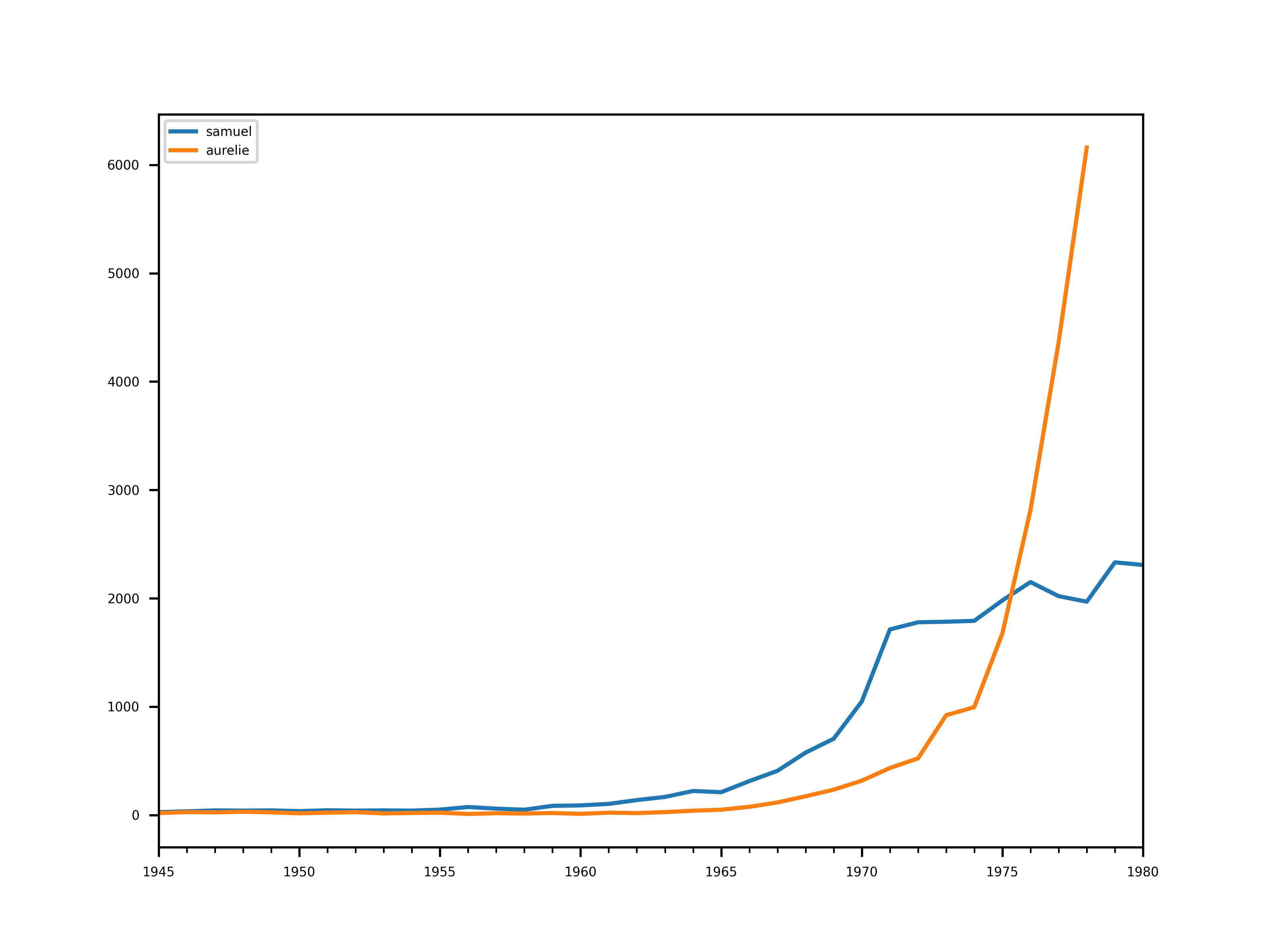
Nous pouvons remarquer deux choses.

  1. le nombre d’occurrences 5 ans avant la naissance d’Aurélie est déjà très élevé (autour de 6000).
  2. la montée des Aurélie (de 500 à 6000 en moins de 10 ans, soit une pente d’environ 500 naissances par an) est plus fulgurante que celle des Samuel (de 500 à 2000 en ~15 ans, soit une pente d’environ 100 prénoms par an).

Recherche de prénoms avec les même tendances

Essayons de trouver les prénoms dont le dernier nombre de naissances est autour des 2000, avec une pente au moins inférieure à 200 prénoms par an.

last_value = sample.iloc[-1, :]
prev_value = sample.iloc[-10, :]
candidates = last_value[(last_value < 3000) & (last_value > 1000)]
candidates = sample[candidates.index]
candidates

            aaron  adrien  alexandre  alexis  amine  antoine  ...  timothee   tom  valentin  victor  yanis  younes
1945-12-31      0     167        209     109      0      888  ...         3     0        36     296      0       0
1946-12-31      0     194        299     143      0     1085  ...         3     0        50     324      0       0
1947-12-31      0     184        303     158      0     1035  ...         6     3        43     295      0       0
1948-12-31      0     214        283     127      0     1152  ...         5     0        47     287      0       0
1949-12-31      3     198        254     124      0     1184  ...         7     0        44     288      0       0
...           ...     ...        ...     ...    ...      ...  ...       ...   ...       ...     ...    ...     ...
2011-12-31   1761    1487       2325    2464   1263     2821  ...      2120  3861      2086    1803   3499     902
2012-12-31   1724    1467       2104    2115   1260     2448  ...      2067  3544      1916    1875   3073    1052
2013-12-31   1908    1238       1970    1832   1150     2283  ...      2104  3209      1997    1934   2547     998
2014-12-31   2053    1310       1813    1775   1141     2217  ...      1956  3107      1948    2059   2359    1097
2015-12-31   2159    1155       1736    1615   1021     2105  ...      1806  2982      1932    2028   2153    1022

[71 rows x 51 columns]

Il reste 51 candidats.

Regardons ceux dont la montée n’est pas trop fulgurante, en comparant la valeur 5 ans plus tôt.

match = candidates.iloc[-1, :] - candidates.iloc[-5, :]
values = match / 5. < 200
candidates = candidates[values[values].index]
candidates.describe()

             aaron       adrien    alexandre       alexis  ...     valentin       victor        yanis       younes
count    71.000000    71.000000    71.000000    71.000000  ...    71.000000    71.000000    71.000000    71.000000
mean    244.014085  1530.535211  3703.422535  1903.915493  ...  1376.746479   970.154930   954.366197   229.366197
std     564.004724  1597.291572  3151.789273  1931.245777  ...  1831.719822   883.522118  1412.619878   309.379067
min       0.000000    59.000000   209.000000   102.000000  ...    27.000000   189.000000     0.000000     0.000000
25%       0.000000   122.500000   389.500000   190.000000  ...    47.500000   276.500000     0.000000     4.000000
50%       6.000000  1155.000000  3079.000000  1242.000000  ...   123.000000   354.000000   143.000000   103.000000
75%      74.000000  2780.500000  6652.000000  3101.000000  ...  2247.500000  1885.500000  1444.000000   344.500000
max    2159.000000  4595.000000  9011.000000  6010.000000  ...  5777.000000  2767.000000  4715.000000  1097.000000

[8 rows x 50 columns]

Seul un prénom a été écarté…

plt.figure()
candidates.plot()
save("candidates_hyp_1")

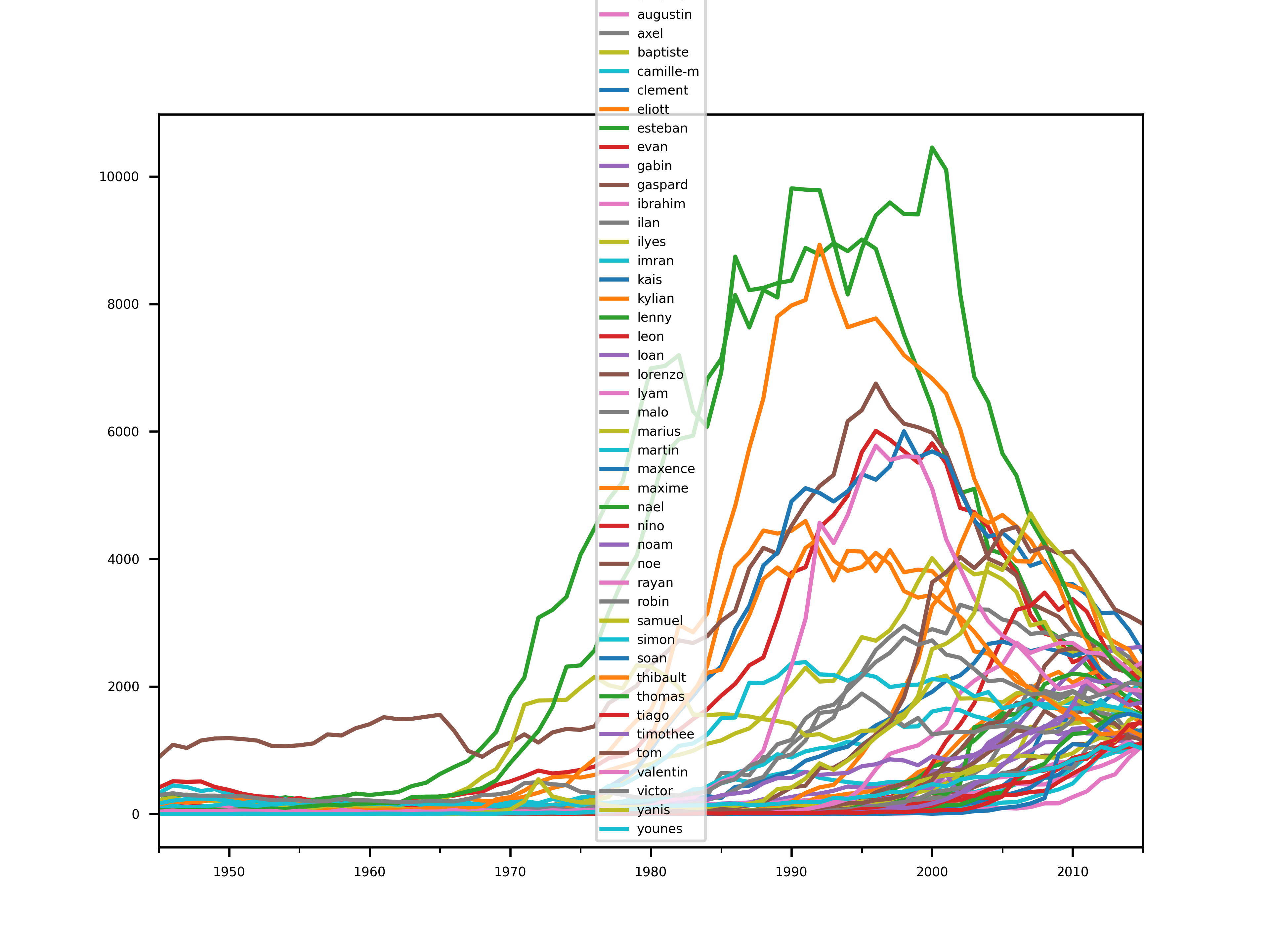
Ceci donne une première liste de prénoms intéressants à consulter.

On remarque que certains d’entre eux ont été très populaires par le passé (plus de 10000 en 2000).

Hypothèse : Les prénoms qui ont été populaires

Maintenant, considérons une autre propriété du prénom Samuel : il n’a jamais été « très » populaire. Dans le sens où il n’a jamais dépassé les 3000 occurrences.

Je vais essayer ici de me concentrer sur ceux dont le nombre de naissances est resté toujours raisonnablement bas (< 3000).

plt.figure()
candidates[candidates < 3000].dropna(axis=1).plot()
save("small_ones")

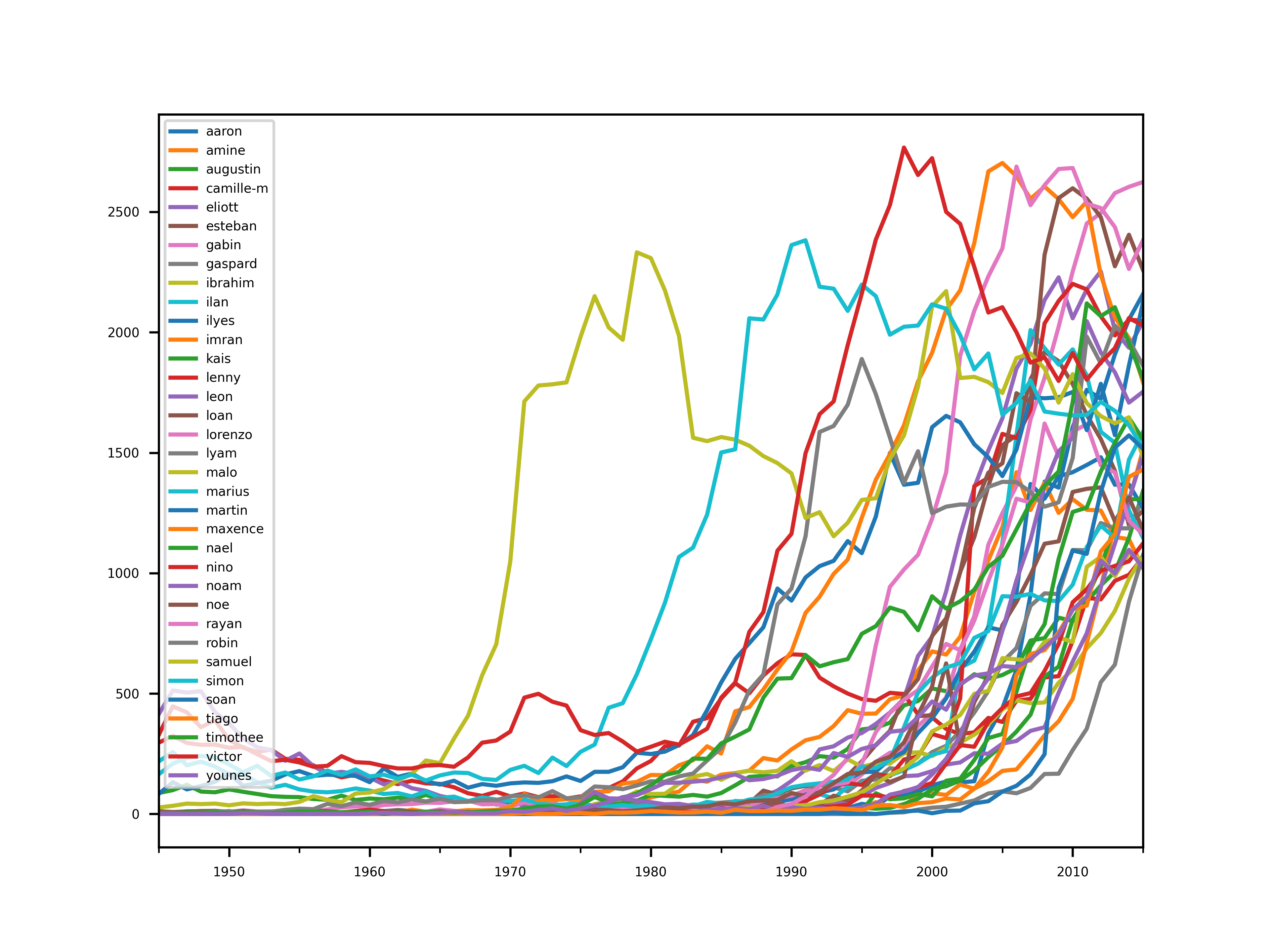
Ces prénoms font aussi de bons candidats. On repère d’ailleurs que beaucoup sont en commun avec la liste précédente.

Tentative de falsification de la prédiction de la tendance des prénoms

Ces hypothèses sont alléchantes, mais elles reposent sur l’idée qu’on peut prédire la tendance d’un prénom avec des données qui remontent à 5 ans avant la naissance.

Peut-on vraiment, en regardant la tendance d’un prénom 5 ans avant la naissance, prédire la fulgurance de sa popularité ?

Cherchons donc comment montrer que cette hypothèse est fausse.

Pour nous en faire une idée, nous pouvons regarder les prénoms que nous trouvons « trop populaire » et les étudier sur la période allant jusqu’à 5 ans avant le pic et observer si nous arrivons réellement à écarter ces prénoms avec le critère de pente et de dernier nombre d’occurrences.

L’hypothèse peut se formaliser comme suit.

Pour démontrer cette hypothèse fausse, nous cherchons à trouver un pic (conclusion fausse) dont la pente est faible et le nombre d’occurrences aussi (prémisses vraies).

Regardons donc les tendances des prénoms très populaires dans les 5 années qui précédent le pic.

Tout d’abord, trouvons les prénoms très populaires. Considérons qu’un prénom est très populaire s’il contient au moins 10K naissances à une année.

plt.figure()
populars = ts_data[(ts_data[ts_data > 10000]).dropna(how="all", axis=1).columns]
populars.plot()
save("populars")

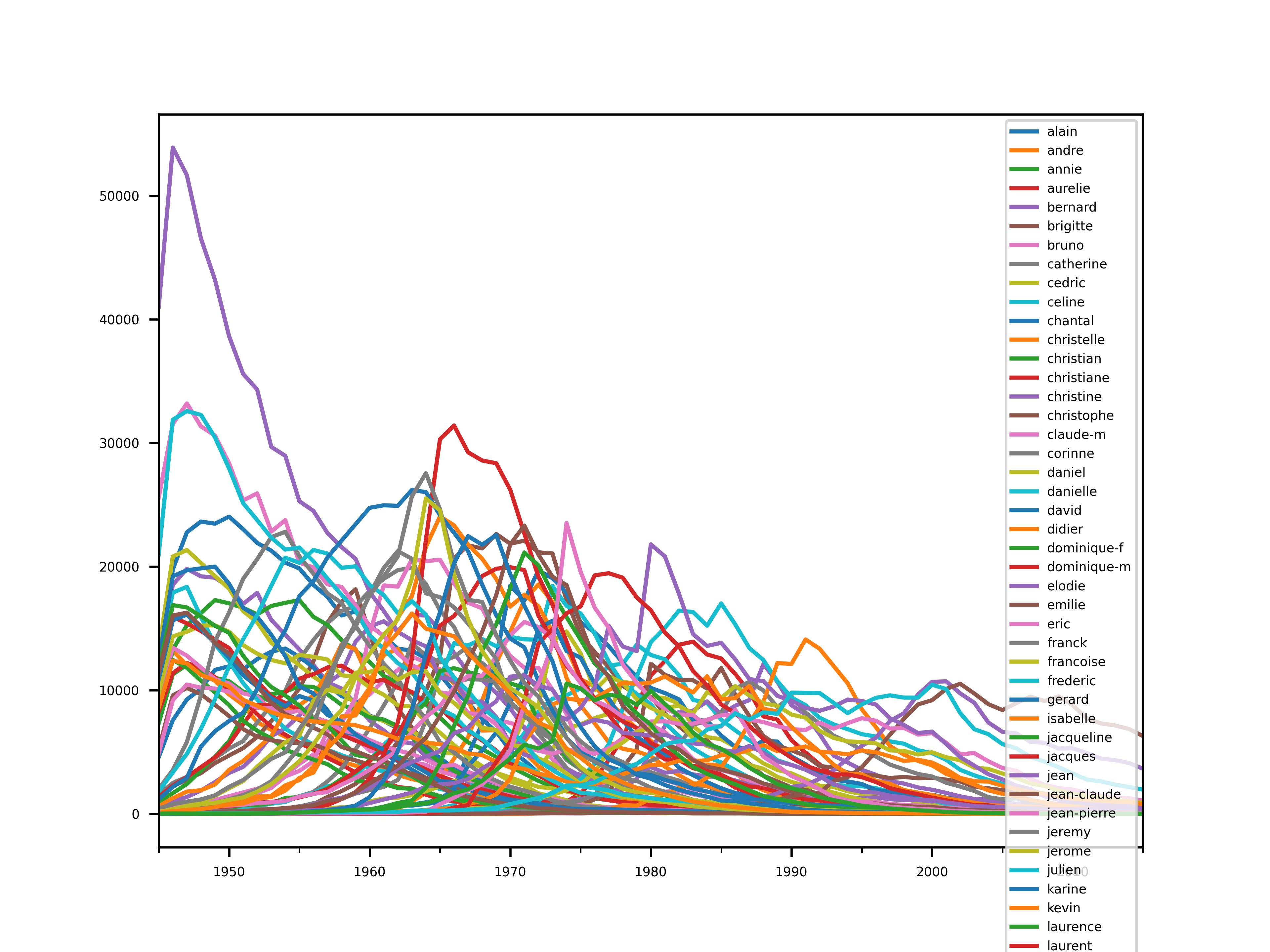
Nous pouvons en profiter pour remarquer le prénom Jean, ayant le record de pic de popularité, avec environ 53000 occurrences en 1946.

Étude de la pente

Nous étudions la pente avec la fonction suivante.

def analyse_slope(duration):
    def slope(serie):
        idxmax = serie.argmax()
        if idxmax < 2*duration:
            return
        return (serie.iloc[idxmax - duration] - serie.iloc[idxmax - 2 * duration]) / duration
    return slope

Voici donc les prénoms populaires et leur pente, 5 ans avant le pic. La barre de 200 permet de voir les prénom répondant au critère.

plt.figure()
populars.apply(analyse_slope(5)).sort_values().plot(kind="bar")
plt.axhline(200)
save("populars_slopes_5")

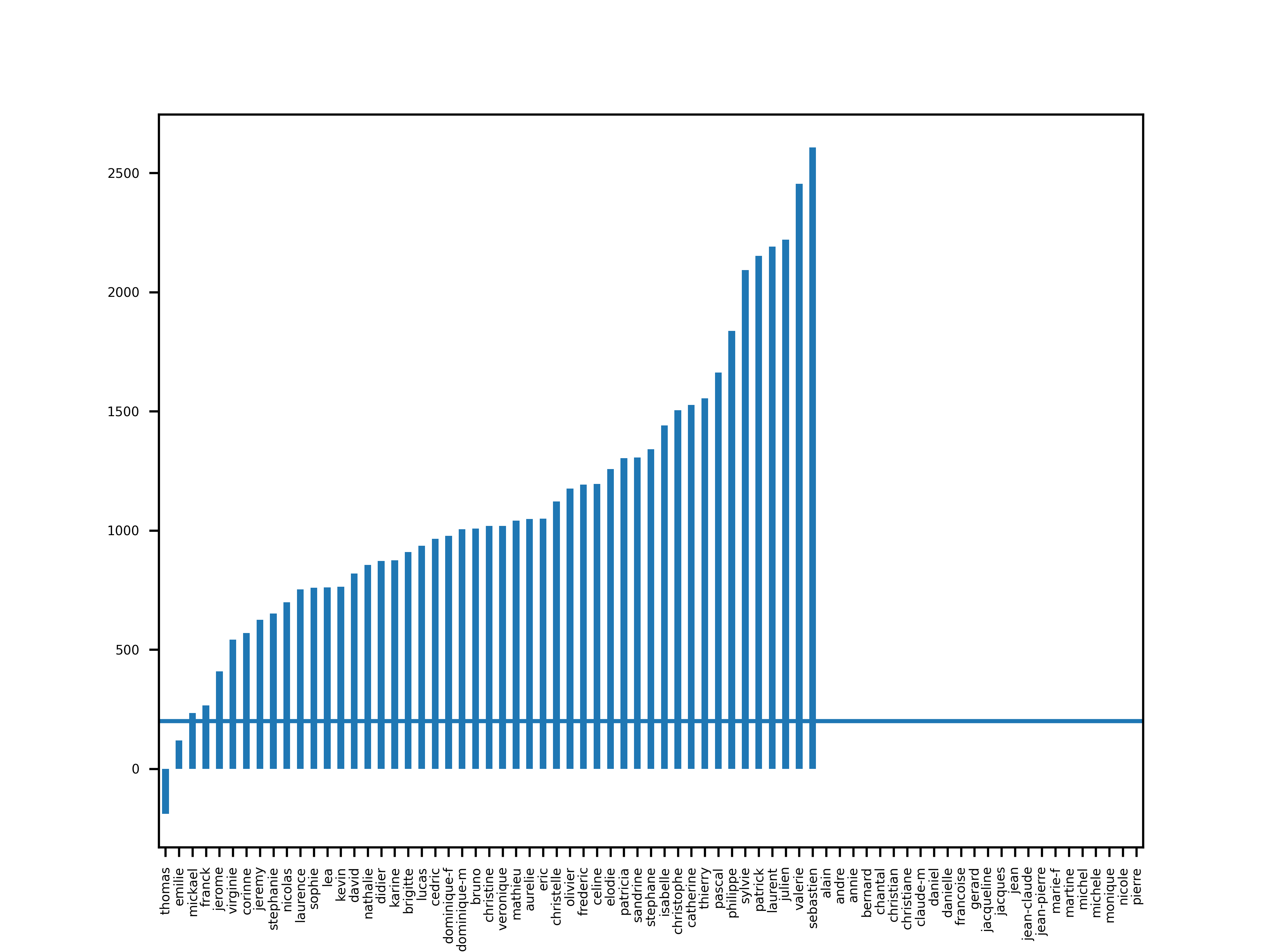
On peut voir que seuls Thomas et Émilie passent l’hypothèse de la pente.

plt.figure()
hardones = populars.apply(analyse_slope(5))
populars[hardones[hardones < 200].index].plot()
save("hardones")

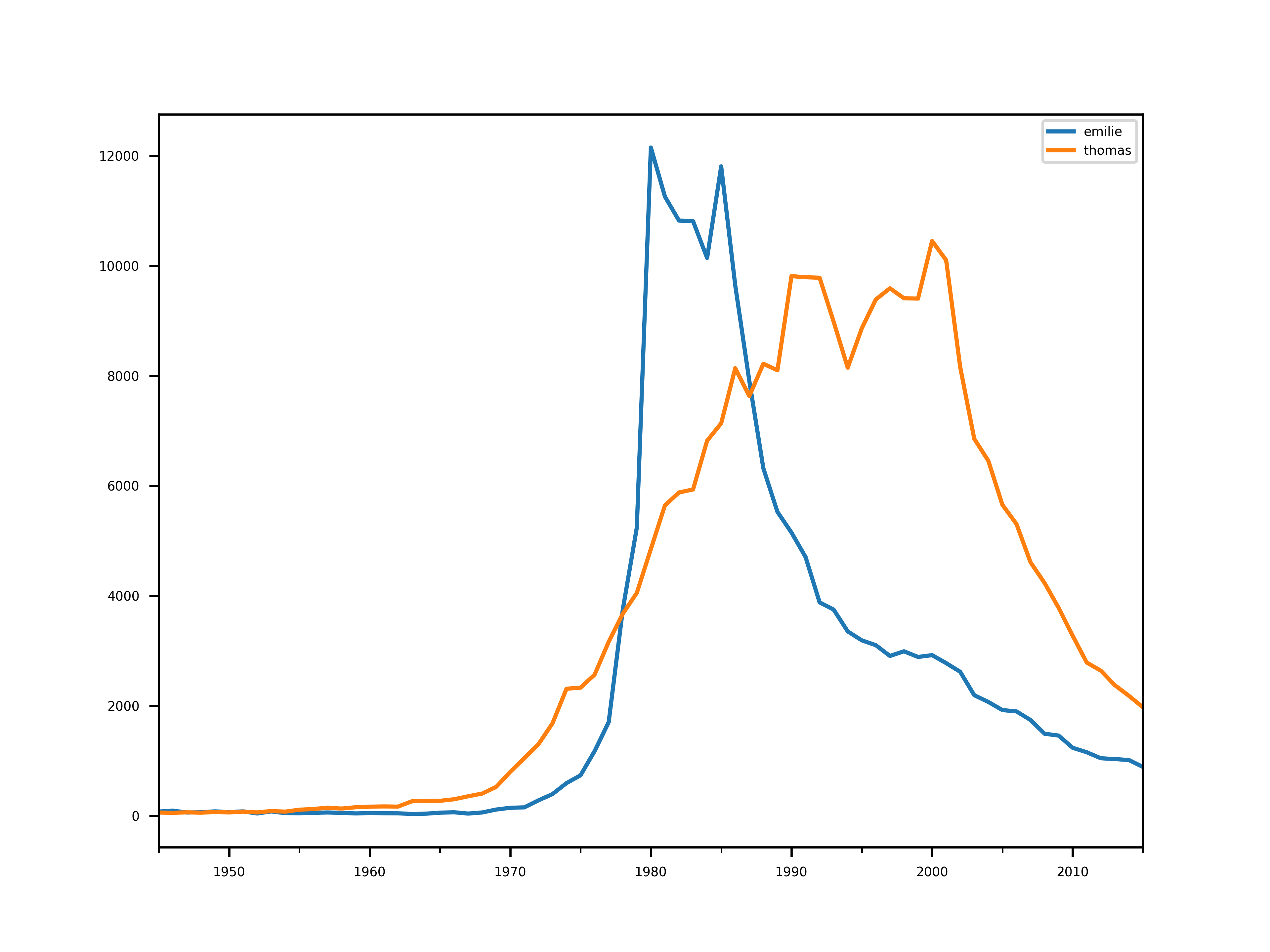
Étude du nombre de naissances à la fin

En ajoutant le critère de nombre de naissances.

def analyse_last_value(duration):
    def last_value(serie):
        idxmax = serie.argmax()
        if idxmax < duration:
            return
        return serie.iloc[idxmax - duration]
    return last_value

Voici donc les prénoms populaires et leur dernière valeur, 5 ans avant le pic. La barre de 3000 permet de voir les prénom répondant au critère.

plt.figure()
populars.apply(analyse_last_value(5)).sort_values().plot(kind="bar")
plt.axhline(3000)
save("populars_last_value_5")

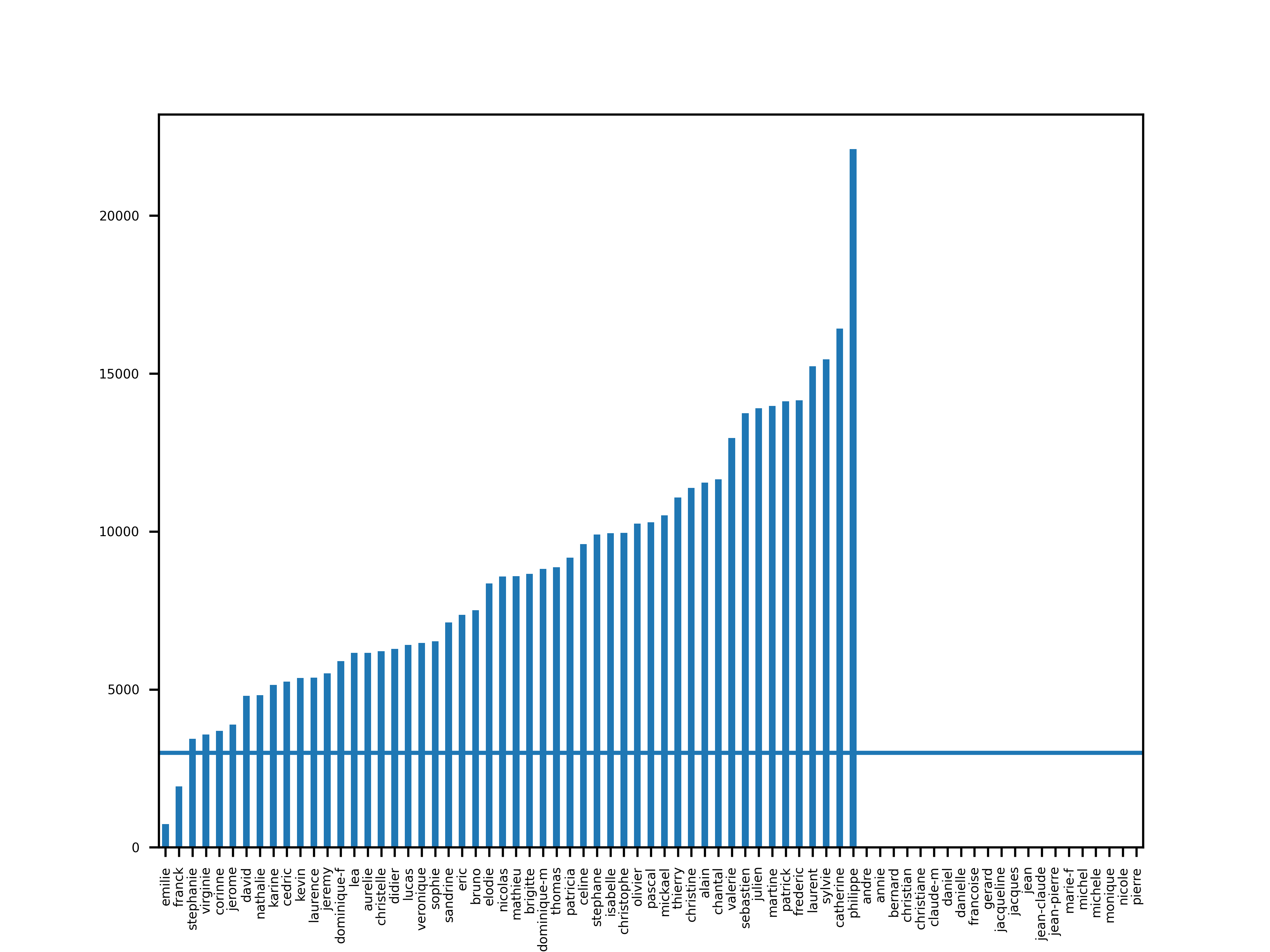
On voit que Émilie et Franck passent au travers de ce critère.

Conclusion

Notre critère ne tiens pas la route, car il n’aurait pas pu prédire la fulgurante popularité d’Émilie.

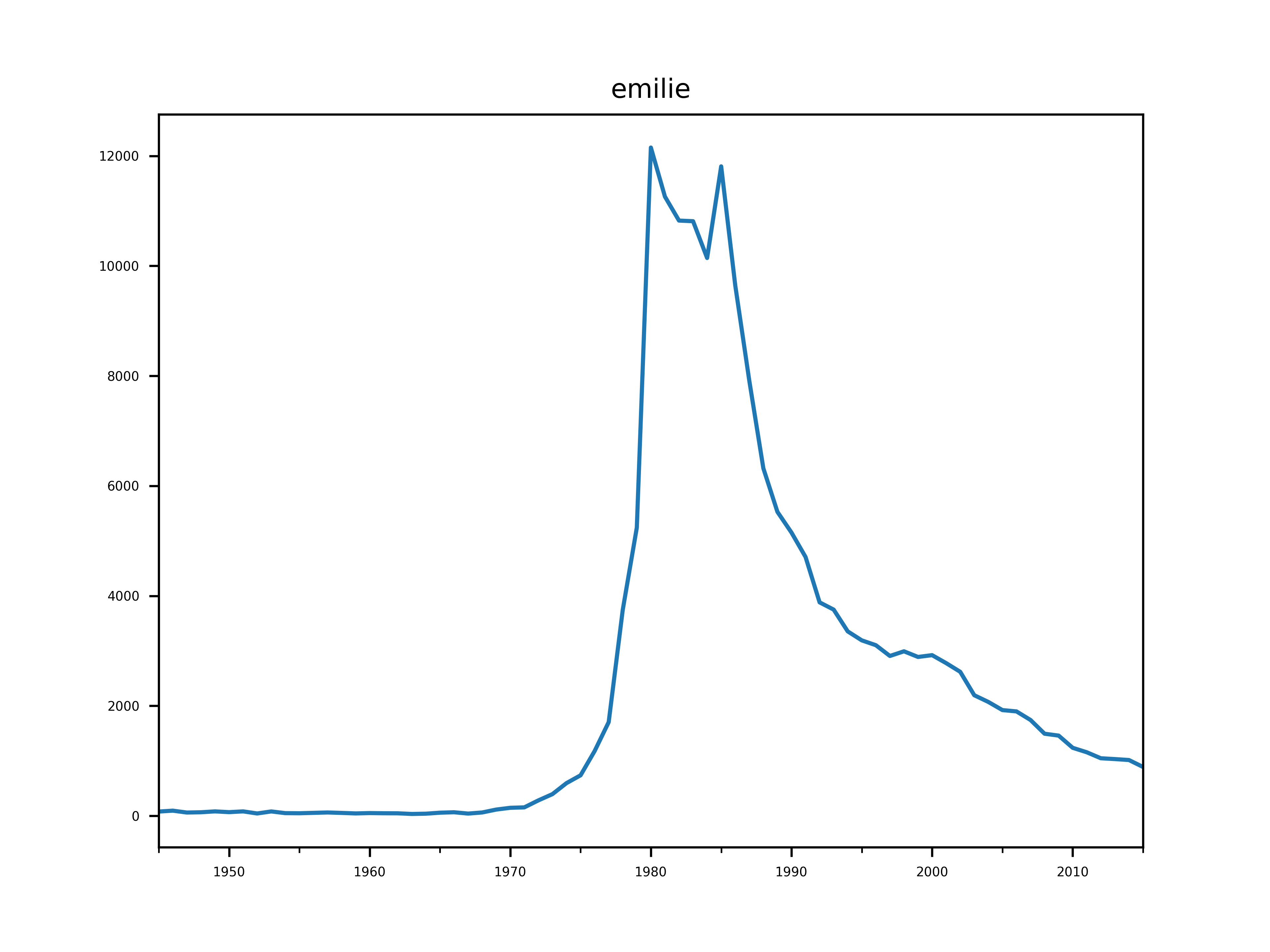
Cependant, il aurait filtrer tous les autres.

Hypothèse des prénoms anciennement populaires

Revenons une dernière fois le prénom de référence : Samuel.

On remarque qu’en 1987, le prénom à déjà « bien vécu ». Il à connu sa popularité 10 ans plus tôt.

Posons l’hypothèse qu’on aime son prénom quand il est encore ancré dans l’inconscient collectif par une popularité marqué dans le passé proche de la naissance. Mais dont le nombre de naissances n’est plus si important que cela.

Cherchons des prénoms correspondant à ce critère. Dont la popularité reste raisonnable (<3000) mais étant populaire un passé proche (autours de 2005 pour nous).

candidates = (
    (sample.max() < 3000) # not too popular
    &
    (sample.max() > 1000) # but still a bit
    &
    (sample.idxmax() > datetime(year=2000, month=1, day=1)) # not too soon early
    &
    (sample.idxmax() < datetime(year=2010, month=12, day=31)) # not too late
)
oldpopular = sample[candidates[candidates].index]

plt.figure()
oldpopular.plot()
save("old_popular")

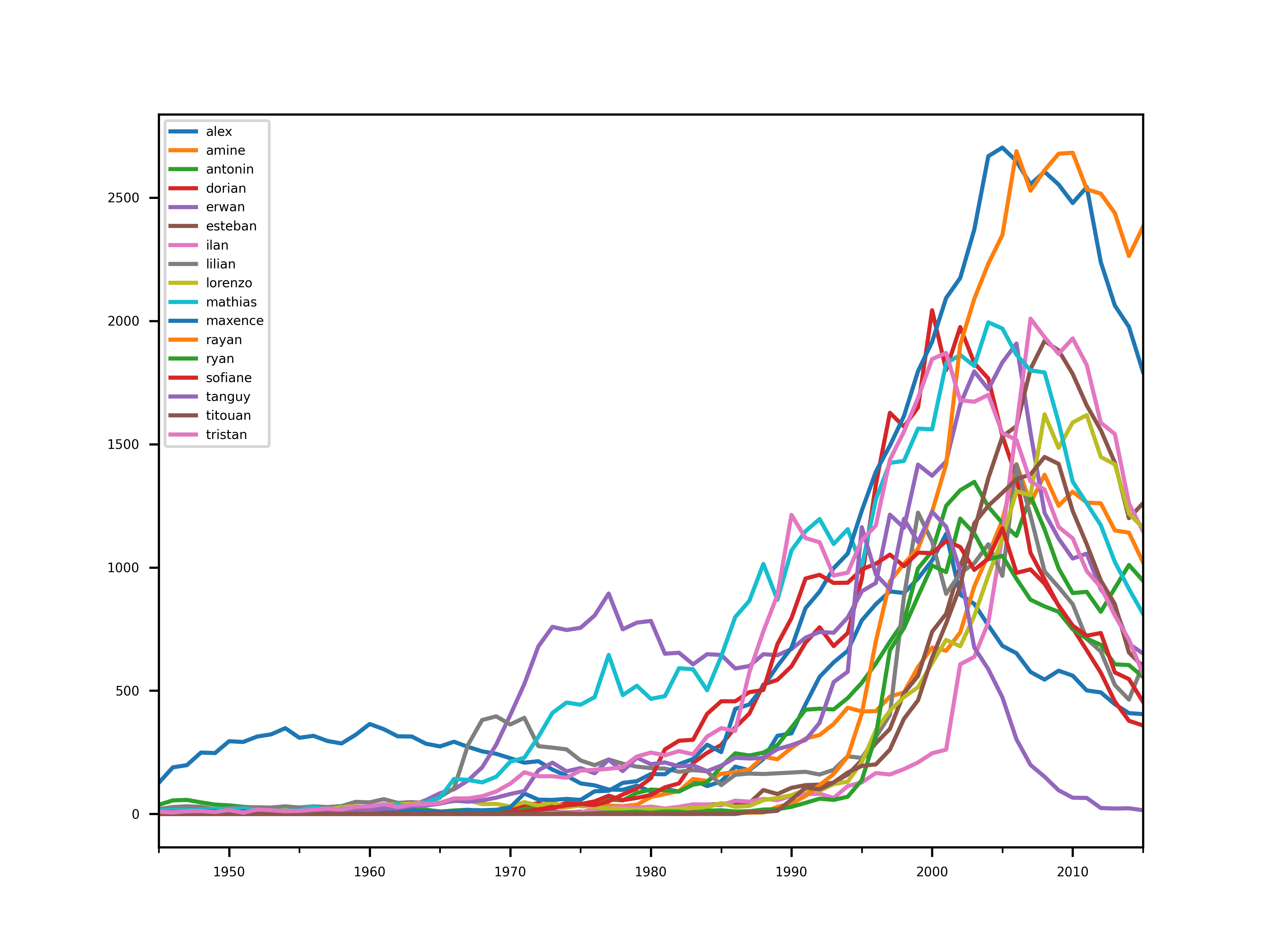
Cette liste est très différente de la précédente et donne une autre piste de réflexion.

Conclusion

Nous avons discuté du souhait de trouver un prénom qui sera agréable à porter pour un petit garçon né en 2021. Nous avons, sur la base de deux témoignages, considérés deux exemples de prénoms, l’un étant présupposé désagréable par sa popularité, l’autre présupposé plus agréable par son aspect plus commun.

Sur la base de l’hypothèse que la popularité d’un prénom impacte effectivement le plaisir à le porter, nous avons fouillé dans une base de données de naissances par année les tendances de prénoms, pour essayer de sortir ceux qui seraient favorables et ceux qui ne le seraient pas.

Nous avons vu que les critères retenus permettaient bien de filtrer la plupart des prénoms considérés problématiques, mais n’avons pas étudié s’ils filtraient trop de prénoms.

Puis, nous avons recherché une autre piste de suggestion, sur la base des prénoms anciennement populaires. aaaaaa Enfin, comme il s’agit d’un exercice pour m’amuser avant tout, et que je commence à être fatigué, je décide de m’arrêter là et d’aller potasser des livres de prénoms :-).

[2021-01-23 Sat] Update

On l’a finalement appelé Sirius…